
- DAZ.online
- DAZ / AZ
- DAZ 12/2009
- Was sucht das Lateinische...
Feuilleton
Was sucht das Lateinische Quadrat im Europäischen Arzneibuch?
Das Wesen des Lateinischen Quadrates hat bereits im 18. Jahrhundert der weltberühmte Basler Mathematiker Leopold Euler (1701– 1783) beschrieben und kommentiert. Im 20. Jahrhundert wurde es von Ronald Aylmer Fisher (1890 – 1962) in die statistische Methodenlehre und Biometrie eingeführt. Dazu werden orthogonale Lateinische Quadrate benötigt, mit deren Hilfe man Simultanvergleiche anstellen kann, die bei relativ geringem Aufwand differenzierte Aussagen ermöglichen.
Zwei orthogonale Lateinische Quadrate derselben Ordnung besitzen gleich viele Felder und die Eigenschaft, dass beim Übereinanderlegen der beiden Quadrate jedes Element des einen mit jedem Element des anderen genau und nur je einmal zusammentrifft.
Statistische Auswertung
Das Europäische Arzneibuch (Pharm. Eur. 6.0) enthält im Kapitel "5.3 Statistische Auswertung" den Abschnitt "8.6 Lateinisches Quadrat" (Band 1, Seite 864). Dort ist beschrieben und graphisch dargestellt, wie aus einer zufälligen Permutation von sechs möglichen Behandlungen (diese bilden die Elemente S1, S2, S3, T1, T2, T3) durch "Rotation" nach rechts ein einfaches Lateinisches Quadrat erzeugt wird (wir haben das Quadrat hier wegen der besseren Übersichtlichkeit koloriert):
Man schreibe die im Schritt 1 gefundene Permutation in die erste Zeile [des Quadrats]. Die zweite Zeile besteht aus der gleichen Permutation, doch werden alle Behandlungen nach rechts verschoben. Die am weitesten rechts liegende Behandlung kommt auf den ganz links liegenden, nun freien Platz. Dies wird für alle Zeilen wiederholt, bis alle Behandlungen einmal in jeder Spalte vorhanden sind.
An dieser Stelle könnte man fragen: "Was muss ein Pharmazeut denn noch alles wissen"?
Wir wollen festhalten:
- Sein Beruf ist interdisziplinär.
- Seine Ausbildung ist fächerübergreifend.
- Er muss die Eigenschaften eines Spezialisten und eines Generalisten in sich vereinen, woraus sich Vor- und Nachteile ergeben.
- Die Breite der Ausbildung umfasst viele spezifische Aspekte.
- Sie ist das Gerüst, das die Entwicklung einer reichen beruflichen Vielfalt ermöglicht.
Doch zurück zum Arzneibuch und zum Begriff "Permutation":
Permutation
Der von lat. permutare = tauschen, aus- oder vertauschen abgeleitete Begriff ist mit Vertauschung, Austausch, Umstellung zu übersetzen und begegnet uns in der Mathematik, den Sprachwissenschaften und der Musik.
In der Mathematik ist eine Permutation eine bijektive Selbstabbildung einer in der Regel endlichen Menge. Man versteht darunter die Veränderung der Anordnung einer Menge durch Vertauschen ihrer Elemente.
Eine praktische Anwendung ist die Konstruktion der Lateinischen Quadrate (s. u.).
In der Sprache kann die Permutation von Satzteilen entweder ohne Veränderung der syntaktischen Funktion erfolgen (A) oder zur (völligen) Änderung der Aussage führen (B).
Beispiele zu A:
Sie trafen sich am Abend.
Am Abend trafen sie sich.
Die Flut kam am frühen Morgen.
Am frühen Morgen kam die Flut.
Vor dem Essen sollt ihr die Hände waschen!
Ihr sollt die Hände vor dem Essen waschen!
Ihr sollt die Hände waschen vor dem Essen!
Beispiele zu B:
Der Sohn von Grete wurde geschlagen.
Der Sohn wurde von Grete geschlagen.
Die Schwester von Hans wird ständig belästigt.
Die Schwester wird ständig von Hans belästigt.
Ihr sollt arbeiten, nicht betteln!
Ihr sollt betteln, nicht arbeiten!
In der polyphonen Musik bedeutet Permutation den Austausch und die wechselnde Kombination kontrapunktischer Elemente. Eine Fuge mit mehreren regelmäßigen Permutationen (Durchführungen), bei der die Kontrapunkte beibehalten und in feststehender Reihenfolge durch alle Stimmen geführt werden, nennt man Permutationsfuge. Um konkret zu werden, betrachten wir die Takte 10 bis 32 im Chor der Kriegsknechte "Lasset uns den nicht zerteilen" aus der Johannes-Passion von Johann Sebastian Bach (Abb. 1).
Lateinische Quadrate
Lateinische Quadrate bestehen aus gleich vielen (= n) waagerechten und senkrechten Feldern, wobei jedes Feld ein Symbol enthält und jedes Symbol in jeder Zeile und jeder Spalte nur einmal auftritt. Die Zahl n bestimmt die Ordnung des Lateinischen Quadrats.
Eine alternative Definition lautet: Ein Lateinisches Quadrat der Kantenlänge n enthält n unterschiedliche Symbole (Elemente), wobei in jeder Zeile und jeder Spalte eine Permutation der n Symbole erfolgt.
Der Name "Lateinisches Quadrat" kommt daher, dass der legendäre Mathematiker Leonhard Euler, als er sich mit diesem Thema befasste, die Buchstaben des Lateinischen Alphabets als Symbole benutzte. Ihm zu Ehren heißen die Lateinischen Quadrate synonym Eulersche Quadrate.
Ein Lateinisches Quadrat der Ordnung 4 (n = 4) enthält vier verschiedene Symbole bzw. Elemente wie Farben, Zahlen oder Buchstaben (Abb. 2).
Erfolgt die Permutation der n Symbole durch Rotation nach rechts (wie auch im Arzneibuch, s. o.), d. h. dass die jeweils vorangehende Zeile um eins nach rechts verschoben wird und das äußerste rechte Symbol der vorangehenden Zeile, das dabei aus dem Quadrat fallen würde, in der neuen Zeile ganz links eingetragen wird, so entsteht ein Lateinisches Quadrat, in dem das erste Symbol mit seinen Kopien eine Diagonale von links oben nach rechts unten bildet. Siehe rote Markierung!
Die erste Zeile von links nach rechts gelesen und die rechte Spalte von oben nach unten gelesen, ergeben zusammen ein Palindrom. Beispiele:
1-2-3-4-3-2-1 oder
A-B-C-D-C-B-A oder
Als Standardquadrat wird ein Lateinisches Quadrat dann bezeichnet, wenn die n Elemente (Symbole) in der ersten Zeile und in der linken Spalte in der gleichen (alphabetischen) Reihenfolge angeordnet sind. Man erhält es durch Rotation nach links (Abb. 3).
Im Standardquadrat verläuft die Diagonale aus gleichen Symbolen von rechts oben nach links unten. Siehe blaue Markierung!
Die erste Spalte von unten nach oben gelesen und die erste Zeile von links nach rechts gelesen ergeben zusammen ein Palindrom, beispielsweise
4-3-2-1-2-3-4 oder
D-C-B-A-B-C-D oder
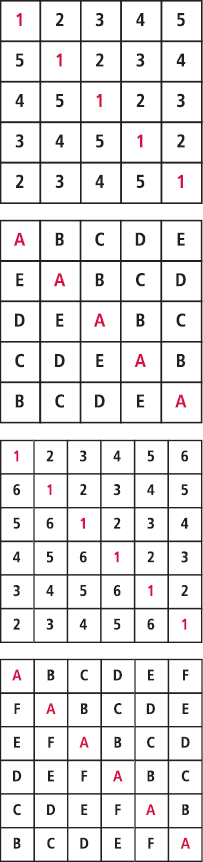
Lateinische Quadrate der Ordnung 5 und 6 sind in Abbildung 4 wiedergegeben.
Umsetzung eines Lateinischen Quadrats der Ordnung 4 in einen verbalen Kanon mit dem Titel "Warnung":
| habet acht | Böses wacht |
seid parat |
Übles naht |
Übles naht |
habet acht |
Böses wacht |
seid parat |
seid parat |
Übles naht |
habet acht |
Böses wacht |
Böses wacht |
seid parat |
Übles naht |
habet acht |
Analoge Umsetzung des Standardquadrates:
habet acht |
Böses wacht |
seid parat |
Übles naht |
Böses wacht |
seid parat |
Übles naht |
habet acht |
seid parat |
Übles naht |
habet acht |
Böses wacht |
Übles naht |
habet acht |
Böses wacht |
seid parat |
Umsetzung eines Lateinischen Quadrats der Ordnung 5 in einen verbalen Kanon mit dem Titel "Aufmunterung":
|
freut Euch
des Lebens
|
Trübsinn
vergebens
|
der Mut
überlebt
|
bleibet doch
munter
|
alles wird
bunter
|
|
alles wird
bunter
|
freut Euch
des Lebens
|
Trübsinn
vergebens
|
der Mut
überlebt
|
bleibet doch
munter
|
|
bleibet doch
munter
|
alles wird
bunter
|
freut Euch
des Lebens
|
Trübsinn
vergebens
|
der Mut
überlebt
|
|
der Mut
überlebt
|
bleibet doch
munter
|
alles wird
bunter
|
freut Euch
des Lebens
|
Trübsinn
vergebens
|
|
Trübsinn
vergebens
|
der Mut
überlebt
|
bleibet doch
munter
|
alles wird
bunter
|
freut Euch
des Lebens
|
Umsetzung eines Lateinischen Quadrats der Ordnung 6 in einen verbalen Kanon mit dem Titel "Nach der Sintflut":
Wasser sinkt |
Nebel fällt |
Sicht erhellt |
Jubel klingt |
Hoffnung kommt |
Glaube frommt |
Glaube frommt |
Wasser sinkt |
Nebel fällt |
Sicht erhellt |
Jubel klingt |
Hoffnung kommt |
Hoffnung kommt |
Glaube frommt |
Wasser sinkt |
Nebel fällt |
Sicht erhellt |
Jubel klingt |
Jubel klingt |
Hoffnung kommt |
Glaube frommt |
Wasser sinkt |
Nebel fällt |
Sicht erhellt |
Sicht erhellt |
Jubel klingt |
Hoffnung kommt |
Glaube frommt |
Wasser sinkt |
Nebel fällt |
Nebel fällt |
Sicht erhellt |
Jubel klingt |
Hoffnung kommt |
Glaube frommt |
Wasser sinkt |
Autor
Prof. Dr. rer. nat. Dr. h. c. Hermann J. Roth
Friedrich-Naumann-Str. 33, 76187 Karlsruhe




















0 Kommentare
Das Kommentieren ist aktuell nicht möglich.